Формулы тетраэдра

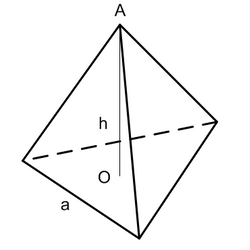
Свойства тетраэдра

• Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед
• Отличительным свойством тетраэдра является то, что медианы и бимедианы фигуры встречаются в одной точке. Важно, что последняя делит медианы в отношении 3:1, а бимедианы - пополам
• Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер

Виды тетраэдров

1. Правильный тетраэдр - это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником. У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину
2. Равногранный тетраэдр - это такой тетраэдр, у которого все грани треугольники равны
3. Ортоцентрический тетраэдр - это такой тетраэдр, у которого каждая высота, опущенная из вершины на противоположную грань, пересекается с остальными высотами в одной точке
4. Прямоугольный тетраэдр - это такой тетраэдр, у которого каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине
5. Каркасный тетраэдр - это такой тетраэдр, который соответствует следующим условиям:
   • есть сфера, которая касается каждого ребра
   • суммы длин ребер, что скрещиваются равны
   • суммы двугранных углов при противоположных ребрах равны
   • окружности, которые вписаны в грани, попарно касаются
   • каждый четырехугольник, образующийся на развертке тетраэдра — описанный
   • перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке
6. Инцентрический тетраэдр - это такой тетраэдр, у которого отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке

Формула высоты тетраэдра

$$ AO = {\sqrt{2 \over 3}} * a $$

Формула объёма тетраэдра

$$ V = {\sqrt{2} \over 12} * a^3 $$

Основные формулы для правильного тетраэдра

• Формула площади $$ S = a^2 * \sqrt{3} $$
• Радиус вписанной сферы, R_впис $$ R_{впис} = a * {\sqrt{6} \over 12} $$
• Радиус описанной сферы, R_опис $$ R_{опис} = a * {\sqrt{6} \over 4} $$