Формулы трапеции

1. Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
2. Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
3. Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне

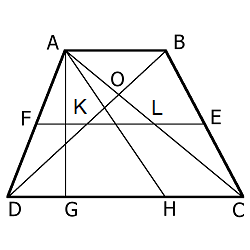
1. Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме $$ FE = {AB + DC \over 2} $$
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
   Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD
3. Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
4. Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
6. Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е. $$ KL = {DC - AB \over 2} $$
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности

1. В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
2. В равнобедренной трапеции длины диагоналей равны (AC = BD)
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная
4. Около равнобедренной трапеции можно описать окружность
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований

Площадь трапеции через основания и высоту

$$ S = {AB + DC \over 2} * AG $$

Площадь трапеции через среднюю линию и высоту

$$ S = FE * AG $$

Площадь трапеции через диагонали и угол между ними

$$ S = {AC * BD \over 2} * sin(∠AOD) = {AC * BD \over 2} * sin(∠AOB) $$

Площадь трапеции через четыре стороны

$$ S = {DC + AB \over 2} * \sqrt{AD^2 - ({(DC - AB)^2 + AD^2 - BC^2 \over 2 * (DC - AB)})^2} $$

Площадь трапеции через стороны

$$ S = {DC + AB \over 2} * \sqrt{AD^2 - {(DC - AB)^2 \over 4}} $$

Площадь трапеции через стороны и угол

$$ S = AD * sin(∠ADC) * (DC - AD * cos(∠ADC)) $$ $$ S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC)) $$

Площадь трапеции через диагонали и угол между ними

$$ S = {AC^2 \over 2} * sin(∠AOD) = {AC^2 \over 2} * sin(∠BOC) $$

Площадь трапеции через среднюю линию, боковую сторону и угол при основании

$$ S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB) $$

Площадь трапеции если в нее вписана окружность

$$ S = {4 * R_В^2 \over sin(∠ADC)} = {4 * R_В^2 \over sin(∠DAB)} $$ $$ S = {AB * DC \over sin(∠ADC)} = {AB * DC \over sin(∠DAB)} $$

Основание через другое основание и среднюю линию

$$ AB = 2 * FE - DC $$ $$ DC = 2 * FE - AB $$

Основание через другое основание, диагонали и угол между ними

$$ DC = {AC * BD \over AG} * sin(∠AOD) - AB $$ $$ AB = {AC * BD \over AG} * sin(∠AOD) - DC $$

Длины сторон

$$ DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ AB = DC - AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD) $$ $$ AB = DC - AD * cos(∠ADC) - BC * cos(∠BCD) $$ $$ AD = {AG \over sin(∠ADC)} $$ $$ BC = {AG \over sin(∠BCD)} $$

Длины сторон

$$ AD = {AG \over sin(∠ADC)} $$ $$ AD = {DC - AB \over 2 * cos(∠ADC)} $$ $$ DC = AB + 2 * AG * ctg(∠ADC) $$ $$ AB = DC - 2 * AG * ctg(∠ADC) $$ $$ DC = AB + 2 * AB * cos(∠ADC) $$ $$ AB = DC - 2 * AB * cos(∠ADC) $$

Длина основания через диагональ, боковую сторону и другое основание

$$ DC = {AC^2 - DA^2 \over AB} $$ $$ AB = {AC^2 - DA^2 \over DC} $$

Длина боковой стороны через диагональ и основания

$$ AD = \sqrt{AC^2 - AB * DC} $$

Длина основания через высоту, другое основание, диагонали и угол между ними

$$ DC = {AC^2 \over AG} * sin(∠AOD) - AB $$ $$ AB = {AC^2 \over AG} * sin(∠AOD) - DC $$

Длина основания через высоту, другое основание и площадь трапеции

$$ DC = {2 * S \over AG} - AB $$ $$ AB = {2 * S \over AG} - DC $$

Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании

$$ AD = {S \over FE * sin(∠ADC)} = {S \over FE * sin(∠DAB)} $$

Длина боковой стороны через площадь трапеции, основания и угол при основании

$$ AD = {2 * S \over (AB + DC) * sin(∠ADC)} $$ $$ AD = {2 * S \over (AB + DC) * sin(∠DAB)} $$

Длины оснований

$$ DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD) $$ $$ AB = DC - BC * cos(∠BCD) = DC - AD * ctg(∠BCD) $$ $$ DC = AB + \sqrt{BC^2 - AD^2} $$ $$ AB = DC - \sqrt{BC^2 - AD^2} $$

Длина основания через боковую сторону, другое основание, диагонали и угол между ними

$$ DC = {AC * BD \over AD} * sin(∠AOD) - AB $$ $$ AB = {AC * BD \over AD} * sin(∠AOD) - DC $$

Длина основания через площадь трапеции, другое основание и высоту

Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG) $$ DC = {2 * S \over AD} - AB $$ $$ AB = {2 * S \over AD} - DC $$

Длина диагоналей через четыре стороны

$$ BD = \sqrt{BC^2 + DC * AB - {DC * (BC^2 - AD^2) \over DC - AB}} $$ $$ AC = \sqrt{AD^2 + DC * AB - {DC * (AD^2 - BC^2) \over DC - AB}} $$

Длина диагоналей по теореме косинусов

$$ BD = \sqrt{DC^2 + BC^2 - 2 * DC * BC * cos(∠BCD)} $$ $$ AC = \sqrt{DC^2 + AD^2 - 2 * DC * AD * cos(∠ADC)} $$

Длина диагоналей через высоту

$$ BD = \sqrt{AG^2 + (DC - AG * ctg(∠BCD))^2} $$ $$ BD = \sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2} $$ $$ BD = \sqrt{DC^2 + BC^2 - 2 * DC * \sqrt{BC^2 - AG^2}} $$ $$ AC = \sqrt{AG^2 + (DC - AG * ctg(∠ADC))^2} $$ $$ AC = \sqrt{AG^2 + (AB + AG * ctg(∠BCD))^2} $$ $$ AC = \sqrt{DC^2 + AD^2 - 2 * DC * \sqrt{AD^2 - AG^2}} $$

Длина диагоналей через стороны и другую диагональ

$$ BD = \sqrt{AD^2 + BC^2 + 2 * DC * AB - AC^2} $$ $$ AC = \sqrt{AD^2 + BC^2 + 2 * DC * AB - BD^2} $$

Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей

$$ BD = {AG * (DC + AB) \over AC * sin(∠AOD)} $$ $$ AC = {AG * (DC + AB) \over BD * sin(∠AOD)} $$ $$ sin(∠AOD) = sin(∠AOB) $$

Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей

$$ BD = {2 * S \over AC * sin(∠AOD)} $$ $$ AC = {2 * S \over BD * sin(∠AOD)} $$ $$ sin(∠AOD) = sin(∠AOB) $$

Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей

$$ BD = {2 * FE * AG \over AC * sin(∠AOD)} $$ $$ AC = {2 * FE * AG \over BD * sin(∠AOD)} $$ $$ sin(∠AOD) = sin(∠AOB) $$

Длина диагоналей через стороны

$$ AC = \sqrt{AD^2 + AB * DC} $$

Длина диагоналей по теореме косинусов

$$ AC = \sqrt{DC^2 + AD^2 - 2 * DC * AD * cos(∠ADC)} $$ $$ AC = \sqrt{DC^2 + AD^2 + 2 * DC * AD * cos(∠DAB)} $$ $$ AC = \sqrt{AB^2 + AD^2 - 2 * AB * AD * cos(∠DAB)} $$ $$ AC = \sqrt{AB^2 + AD^2 + 2 * AB * AD * cos(∠ADC)} $$

Длина диагоналей

$$ AC = \sqrt{AG^2 + FE^2} $$ $$ AC = \sqrt{AG^2 + {(DC + AB)^2 \over 4 }} $$ $$ AC = \sqrt{{AG * (AB + DC) \over sin(∠AOD)}} = \sqrt{{2 * S \over sin(∠AOD)}} = \sqrt{{2 * FE * AG \over sin(∠AOD)}} $$

Длина диагоналей через высоту основание и угол при основании

$$ AC = \sqrt{AG^2 + (DC - AG * ctg(∠ADC))^2} $$ $$ AC = \sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2} $$

Длина диагоналей через сторону и высоту

$$ AC = \sqrt{DC^2 + AD^2 - 2 * DC * \sqrt{AD^2 - AG^2}} $$

$$ BD = \sqrt{AD^2 + AB^2} $$ $$ AC = \sqrt{AC^2 + DC^2} $$

Длина средней линии через основания

$$ FE = {DC + AB \over2} $$

Длина средней линии через основание, высоту и углы при нижнем основании

$$ FE = DC - AG * {ctg(∠ADC) + ctg(∠BCD) \over 2} $$ $$ FE = AB + AG * {ctg(∠ADC) + ctg(∠BCD) \over 2} $$

Длина средней линии через диагонали, высоту и угол между диагоналями

$$ FE = {AC * BD \over 2 * AG} * sin(∠AOD) $$ $$ FE = {AC * BD \over 2 * AG} * sin(∠AOB) $$

Длина средней линии через площадь и высоту

$$ FE = {S \over AG} $$

Длина средней линии через основания

$$ FE = {DC + AB \over2} $$

Длина средней линии через основание, высоту и углы при нижнем основании

$$ FE = DC - AG * ctg(∠ADC) = AB + AG * ctg(∠ADC) $$

Длина средней линии через основания, боковую сторону и высоту

$$ FE = DC - \sqrt{AD^2 - AG^2} = AB + \sqrt{AD^2 - AG^2} $$

Длина средней линии через диагонали, высоту и угол между диагоналями

$$ FE = {AC^2 \over 2 * AG} * sin(∠AOD) = {AC^2 \over 2 * AG} * sin(∠AOB) $$

Длина средней линии через площадь и боковую сторону

$$ FE = {S \over AD * sin(∠ADC)} $$

Длина средней линии через основания, высоту и угол при нижнем основании

$$ FE = DC - AG * {ctg(∠BCD) \over 2} $$ $$ FE = AB + AG * {ctg(∠BCD) \over 2} $$

Длина средней линии через основания, боковую сторону и угол при нижнем основании

$$ FE = DC - BC * {cos(∠BCD) \over 2} $$ $$ FE = AB + BC * {cos(∠BCD) \over 2} $$

Длина средней линии через основания и боковые стороны

$$ FE = DC - {\sqrt{BC^2 - AD^2} \over 2} $$ $$ FE = AB + {\sqrt{BC^2 - AD^2} \over 2} $$

Длина средней линии через диагонали, высоту и угол между диагоналями

$$ FE = {AC * BD \over 2 * AG} * sin(∠AOD) $$ $$ FE = {AC * BD \over 2 * AG} * sin(∠AOB) $$

Длина высоты через четыре стороны

$$ AG = \sqrt{AD^2 - ({(DC - AB)^2 + AD^2 - BC^2 \over 2 * (DC - AB)})^2} $$

Длина высоты через боковую сторону и прилегающий угол к основанию

$$ AG = AD * sin(∠ADC) = BC * sin(∠BCD) $$

Длина высоты через диагонали и углы между ними

$$ AG = {AC * BD \over AB + DC} * sin(∠AOD) $$ $$ AG = {AC * BD \over AB + DC} * sin(∠AOB) $$

Длина высоты через среднюю линию, диагонали и углы между ними

$$ AG = {AC * BD \over 2 * FE} * sin(∠AOD) $$ $$ AG = {AC * BD \over 2 * FE} * sin(∠AOB) $$

Длина высоты через площадь и основания

$$ AG = {2 * S \over AB + DC} $$

Длина высоты через площадь и среднюю линию

$$ AG = {S \over FE} $$

Длина высоты через по сторонам

$$ AG = \sqrt{AD^2 - {(DC - AB)^2 \over 4}} $$

Длина высоты через боковую сторону и прилегающий угол к основанию

$$ AG = AD * sin(∠ADC) $$

Длина высоты через основания и прилегающий угол к основанию

$$ AG = {DC - AB \over 2} * tg(∠ADC) $$

Длина высоты через диагонали и углы между ними

$$ AG = {AC^2 \over AB + DC} * sin(∠AOD) $$ $$ AG = {AC^2 \over AB + DC} * sin(∠AOB) $$

Длина высоты через площадь и основания

$$ AG = {2 * S \over AB + DC} $$

Длина высоты через площадь и среднюю линию

$$ AG = {S \over FE} $$

Сторона AD

Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.

Сторона BC по трём сторонам

$$ BC = \sqrt{AD^2 + (DC - AB)^2} $$

Сторона BC через основания и угол ∠BCD

$$ BC = {DC - AB \over cos(∠BCD)} $$

Сторона BC через Сторону AD

$$ BC = {AD \over sin(∠BCD)} $$

Сторона BC через площадь, среднюю линию и угол ∠BCD

$$ BC = {S \over FE * sin(∠BCD)} $$

Сторона BC через площадь, основания и угол ∠BCD

$$ BC = {2 * S \over (AB + DC) * sin(∠BCD)} $$