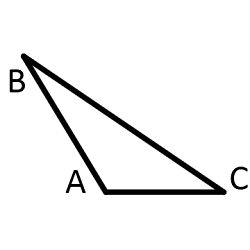
Формулы треугольника
Для расчёта всех основных параметров треугольника воспользуйтесь калькулятором.
Виды треугольников
-
Остроугольный треугольник - это треугольник, в котором все три угла острые, т.е. меньше 90°. -
Прямоугольный треугольник - это треугольник, содержащий прямой угол.
Две стороны, образующие прямой угол, называются катетами (АС и АВ), а сторона, противолежащая прямому углу, называется гипотенузой (ВС).
-
Тупоугольный треугольник - это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.(по числу равных сторон) -
Равносторонний (правильный) треугольник - это треугольник, у которого все стороны и все углы равны (каждый угол равен 60°). -
Равнобедренный тругольник - это треугольник, у которого два угла и две стороны равны. -
Разносторонний треугольник - это треугольник, в котором все углы, а значит и все стороны попарно различны.
Свойства треугольника, применимые к любому треугольнику:
- Против большей стороны лежит больший угол, и наоборот.
- Против равных сторон лежат равные углы, и наоборот. (В частности, все углы в равностороннем треугольнике равны.)
- Сумма углов треугольника равна 180° (Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60°).
- Продолжая одну из сторон треугольника (AВ), получаем внешний угол Θ.
- Любая сторона треугольника меньше суммы двух других сторон и больше их разности:
- $$ AB < BC + CA $$
- $$ AB > BC - CA $$
- $$ BC < AB + CA $$
- $$ BC > AB - CA $$
- $$ CA < AB + BC $$
- $$ CA > AB - BC $$
Признаки равенства треугольников
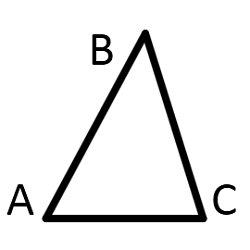  |
Произвольные треугольники равны, если:
|
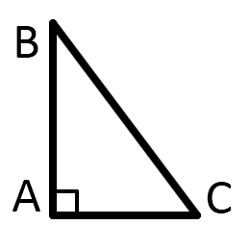 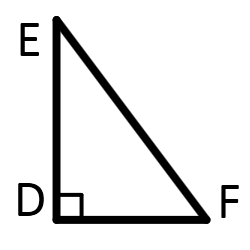 |
Прямоугольные треугольники равны, если равны:
|
Подобные треугольники
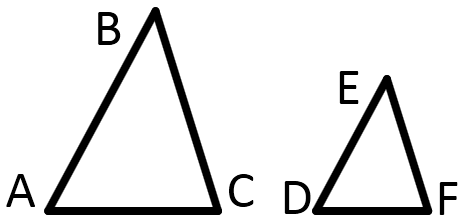
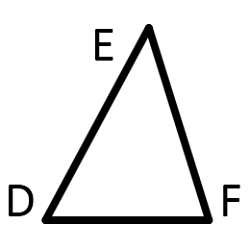
Два треугольника являются подобными, если углы одного треугольника равны, углам тругого треугольника, а стороны подобны
- ∠ABC = ∠DEF и ∠BCA = ∠EFD и ∠CAB = ∠FDE;
- $$ {AB \over DE} = {BC \over EF} = {CA \over FD} = К_{подобия} $$
Признаки подобия треугольников
- Два угла одного треугольника равны двум углам другого треугольника.
- Две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны.
- Три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.
Свойства подобных треугольников.
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия (Kподобия) $$ {S_{ΔABC} \over S_{ΔDEF}} = К_{подобия}^2 $$
- Отношение периметров и длин биссектрис, медиан, высот, серединных перпендикуляров равно коэффициенту подобия. т.е. в подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.
Подобие в прямоугольных треугольниках.
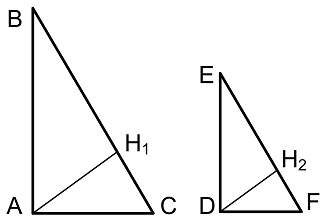
- Треугольники, образованные высотой, опущенной из прямого угла, являются подобными друг другу
- Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
- Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
- Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
Площадь треугольника
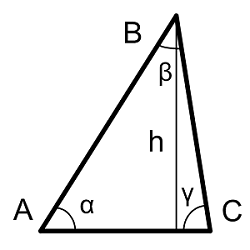
| Где: | AB,BC,AC – стороны треугольника |
| h – высота треугольника | |
| α, β, γ– углы треугольника | |
| P – полупериметр | |
| AC – основание треугольника |
Площадь произвольного треугольника
$$ S = {1 \over 2} * AC * h $$Площадь треугольника по формуле Герона
$$ P = {AB + BC + AC \over 2} $$ $$ S = \sqrt{P * (P - AB) * (P - BC) * (P - AC)} $$Площадь треугольника по углу и двум сторонам
$$ S = {1 \over 2} * AB * AC * sin(α) $$ $$ S = {1 \over 2} * AB * BC * sin(β) $$ $$ S = {1 \over 2} * AC * BC * sin(γ) $$Площадь треугольника по двум углам и стороне
$$ S = {AB^2 \over 2} * {sin(α) * sin(β) \over sin(α + β)} = {AB^2 \over 2} * {sin(α) * sin(β) \over sin(γ)} $$ $$ S = {BC^2 \over 2} * {sin(γ) * sin(β) \over sin(γ + β)} = {BC^2 \over 2} * {sin(γ) * sin(β) \over sin(α)} $$ $$ S = {AC^2 \over 2} * {sin(γ) * sin(α) \over sin(γ + α)} = {BC^2 \over 2} * {sin(γ) * sin(α) \over sin(β)} $$
Площадь прямоугольного треугольника по катетам
| Где: | AB,AC – катеты треугольника |
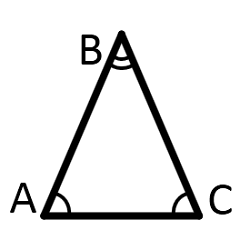
Площадь равнобедренного треугольника
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника |
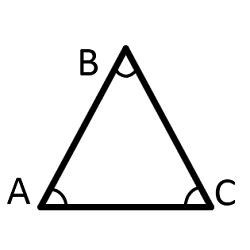
Площадь равностороннего треугольника
| Где: | AB,BC,AC – равные стороны треугольника |
| h – высота треугольника |
Стороны треугольника

| Где: | AB,BC,AC – стороны треугольника |
| h – высота треугольника | |
| α, β, γ– углы треугольника | |
| P – полупериметр | |
| AC – основание треугольника |
Сторона треугольника по двум сторонам и углу
$$ AB = \sqrt{BC^2 + AC^2 - 2 * BC * AC * cos(γ)} $$ $$ BC = \sqrt{AB^2 + AC^2 - 2 * AB * AC * cos(α)} $$ $$ AC = \sqrt{AB^2 + BC^2 - 2 * AB * BC * cos(β)} $$Сторона треугольника по стороне и двум углам
$$ AB = {AC * sin(γ) \over sin(β)} = {AC * sin(γ) \over sin(γ + α)} = {AC * sin(α + β) \over sin(β)} $$ $$ BC = {AB * sin(α) \over sin(γ)} = {AB * sin(α) \over sin(α + β)} = {AB * sin(β + γ) \over sin(γ)} $$ $$ AC = {BC * sin(β) \over sin(α)} = {AB * sin(β) \over sin(β + γ)} = {AB * sin(α + γ) \over sin(α)} $$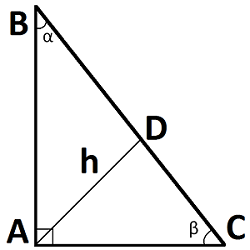
Сторона прямоугольного треугольника
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника |
Сторона прямоугольного треугольника по теореме Пифагора.
$$ BC = \sqrt{AB^2 + AC^2} $$ $$ AB = \sqrt{BC^2 - AC^2} $$ $$ AC = \sqrt{BC^2 - AB^2} $$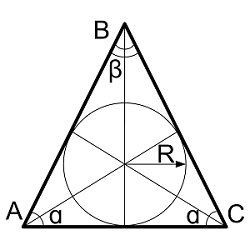
Сторона равнобедренного треугольника
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника |
Высота треугольника
Высота – это перпендикуляр, выходящий из любой вершины треугольника, к противоположной стороне или её продолжению для треугольника с тупым углом. Высоты треугольника пересекаются в одной точке
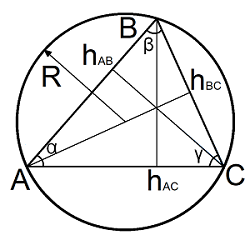
| Где: | AB,BC,AC – стороны треугольника |
| h – высота треугольника | |
| P – полупериметр $$ P = {AB + BC + AC \over 2} $$ | |
| α, β, γ – углы треугольника | |
| R - радиус описанной окружности | |
| S - площадь треугольника |
Высота на сторону АС, hAC
$$ h_{AC} = {2 \over AC} * \sqrt{P * (P - AC) * (P - AB) * (P - BC)} $$Высота на сторону AB, hAB
$$ h_{AB} = {2 \over AB} * \sqrt{P * (P - AC) * (P - AB) * (P - BC)} $$Высота на сторону BC, hBC
$$ h_{BC} = {2 \over BC} * \sqrt{P * (P - AC) * (P - AB) * (P - BC)} $$Формула длины высоты через сторону и угол
Высота на сторону АС, hAC
$$ h_{AC} = AB * sin(α) = BC * sin(γ) $$Высота на сторону AB, hAB
$$ h_{AB} = BC * sin(β) = AC * sin(α) $$Высота на сторону BC, hBC
$$ h_{BC} = AC * sin(γ) = AB * sin(β) $$Формула длины высоты через сторону и площадь
Высота на сторону АС, hAC
$$ h_{AC} = {2 * S \over AC} $$Высота на сторону AB, hAB
$$ h_{AB} = {2 * S \over AB} $$Высота на сторону BC, hBC
$$ h_{BC} = {2 * S \over BC} $$Формула длины высоты через стороны и радиус
Высота на сторону АС, hAC
$$ h_{AC} = {AB * BC \over 2 * R} $$Высота на сторону AB, hAB
$$ h_{AB} = {BC * AC \over 2 * R} $$Высота на сторону BC, hBC
$$ h_{BC} = {AB * AC \over 2 * R} $$Формулы высоты из прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр - точка пересечения высот, совпадает с вершиной прямого угла.

| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| BD, DC – отрезки полученные от деления гипотенузы, высотой | |
| α, β– углы треугольника |
Формула длины высоты через гипотенузу и острые углы
$$ h = BC * sin(α) * cos(α) = BC * sin(β) * cos(β) $$Формула длины высоты через катет и угол
$$ h = AB * sin(α) = AC * sin(β) $$Формула длины высоты через составные отрезки гипотенузы
$$ h = \sqrt{BD * DC} $$Биссектрисы в треугольнике
Биссектриса – это отрезок, который делит угол пополам из которого выходит. Точка пересечения всех трех биссектрис треугольника совпадает с центром вписанной окружности.
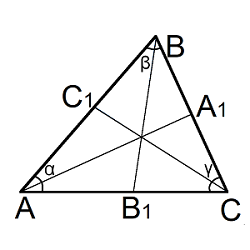
| Где: | AB,BC,AC – стороны треугольника |
| AA1,BB1,CC1 - биссектрисы в треугольнике | |
| α, β, γ– углы треугольника | |
| P – полупериметр $$ P = {AB + BC + AC \over 2} $$ |
Длина биссектрисы через две стороны и угол
$$ BB_1 = {2 * AB * BC * cos(β/2) \over AB + BC} $$ $$ AA_1 = {2 * AB * AC * cos(α/2) \over AB + AC} $$ $$ CC_1 = {2 * BC * AC * cos(γ/2) \over BC + AC} $$Длина биссектрисы через полупериметр и стороны
$$ BB_1 = {2 * \sqrt{AB * BC * P * (P - AC)} \over AB + BC} $$ $$ AA_1 = {2 * \sqrt{AB * AC * P * (P - BC)} \over AB + AC} $$ $$ CC_1 = {2 * \sqrt{BC * AC * P * (P - AB)} \over BC + AC} $$Длина биссектрисы через три стороны
$$ BB_1 = {\sqrt{AB * BC * (AB + BC + AC) * (AB + BC - AC)} \over AB + BC} $$ $$ AA_1 = {\sqrt{AB * AC * (AB + BC + AC) * (AB + AC - BC)} \over AB + AC} $$ $$ CC_1 = {\sqrt{BC * AC * (AB + BC + AC) * (BC + AC - AB)} \over BC + AC} $$Длина биссектрисы через стороны и отрезки, на которые делит биссектриса
$$ BB_1 = \sqrt{AB * BC - AB_1 * B_1C} $$ $$ AA_1 = \sqrt{AB * AC - BA_1 * A_1C} $$ $$ CC_1 = \sqrt{BC * AC - AC_1 * C_1B} $$Формула длины биссектрис в прямоугольном треугольнике
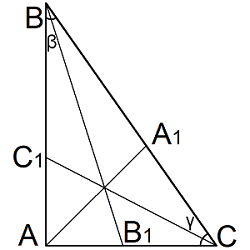
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| β, γ– острые углы треугольника |
Длина биссектрисы из прямого угла, через катеты.
$$ AA_1 = \sqrt{2} * {AB * AC \over AB + AC} $$Длина биссектрисы из прямого угла, через гипотенузу и угол
$$ AA_1 = {2 * BC \over \sqrt{2}} * {sin(γ) * cos(γ) \over sin(γ) + cos(γ)} $$Длина биссектрисы через катет и угол
$$ BB_1 = {AB \over cos(β / 2)} $$ $$ BB_1 = AB * \sqrt{2 \over 1 + sin(γ)} = AB * \sqrt{2 \over 1 + cos(β)} $$ $$ CC_1 = {AC \over cos(γ / 2)} $$ $$ CC_1 = AC * \sqrt{2 \over 1 + sin(β)} = AC * \sqrt{2 \over 1 + cos(γ)} $$Длина биссектрисы через катет и гипотенузу
$$ BB_1 = AB * \sqrt{{2 * BC \over AB * BC}} $$ $$ CC_1 = AC * \sqrt{{2 * BC \over AC * BC}} $$Длина биссектрисы равнобедренного треугольника
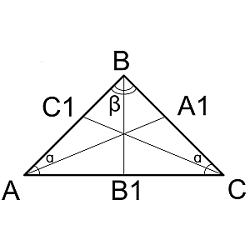
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника | |
| α – равные углы при основании треугольника | |
| β – угол образованный равными сторонами треугольника |
Длина биссектрисы через стороны и угол, равнобедренного треугольника
$$ BB_1 = AB * sin(α) = {AC \over 2} * tg(α) = AB * cos({β \over 2}) $$ $$ BB_1 = AB * \sqrt{{1 + cos(β)} \over 2} $$Длина биссектрисы через стороны, равнобедренного треугольника
$$ BB_1 = \sqrt{{AB^2 - AC^2 \over 4}} $$Длина биссектрисы равностороннего треугольника
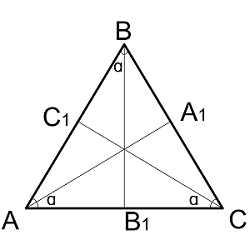
| Где: | AB,BC,AC – равные стороны треугольника |
Медиана в треугольнике
Медиана – это отрезок, который выходит из вершины и делит противоположную сторону пополам. Медиана делит треугольник на два равных по площади треугольника.
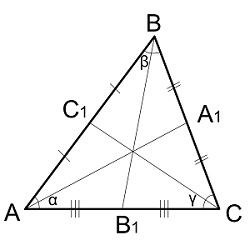
| Где: | AB,BC,AC – стороны треугольника |
| AA1,BB1,CC1 - медианы в треугольнике | |
| α, β, γ– углы треугольника |
Длина медианы через три стороны
$$ BB_1 = {1 \over 2} * \sqrt{2 * AB^2 + 2 * BC^2 - AC^2} $$ $$ AA_1 = {1 \over 2} * \sqrt{2 * AB^2 + 2 * AC^2 - BC^2} $$ $$ CC_1 = {1 \over 2} * \sqrt{2 * BC^2 + 2 * AC^2 - AB^2} $$Длина медианы через две стороны и угол между ними
$$ BB_1 = {1 \over 2} * \sqrt{AB^2 + BC^2 + 2 * AB * BC * cos(β)} $$ $$ AA_1 = {1 \over 2} * \sqrt{AB^2 + AC^2 + 2 * AB * AC * cos(α)} $$ $$ CC_1 = {1 \over 2} * \sqrt{BC^2 + AC^2 + 2 * BC * AC * cos(γ)} $$Длина медианы в прямоугольном треугольнике, выходящая из прямого угла.
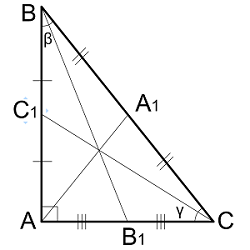
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| AA1,BB1,CC1 - медианы в треугольнике | |
| β, γ– острые углы треугольника |
Длина медианы в прямоугольном треугольнике, выходящая из прямого угла, равна радиусу описанной окружности, а середина гипотенузы является центром описанной окружности
$$ AA_1 = R = {BC \over 2} $$Длина медианы через катеты
$$ AA_1 = {1 \over 2} * \sqrt{AB^2 * AC^2} $$Длина медианы через катет и острый угол
$$ AA_1 = {AB \over 2 * sin(β)} = {AC \over 2 * cos(β)} $$Описанная окружность
Радиус описанной окружности произвольного треугольника по сторонам
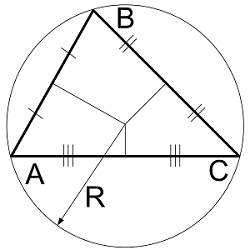
| Где: | AB,BC,AC – стороны треугольника |
| P – полупериметр $$ P = {AB + BC + AC \over 2} $$ | |
| R - радиус описанной окружности |
Радиус описанной окружности равностороннего треугольника по стороне или высоте
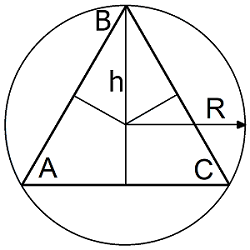
| Где: | AB,BC,AC – равные стороны треугольника |
| h – высота треугольника | |
| R - радиус описанной окружности |
Радиус описанной окружности равнобедренного треугольника по сторонам
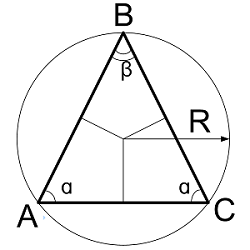
| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника | |
| h – высота треугольника | |
| R - радиус описанной окружности |
Радиус описанной окружности прямоугольного треугольника по катетам
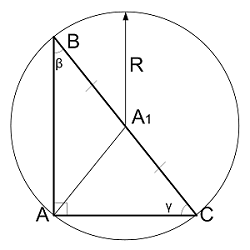
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| R - радиус описанной окружности |
Длина окружности, L
$$ L = 2 * \pi * R $$Площадь окружности, S
$$ S = \pi * R^2 $$Вписанная окружность
Радиус вписанной окружности произвольного треугольника по сторонам
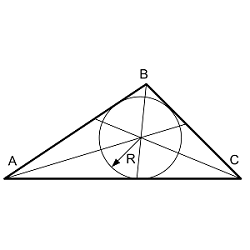
| Где: | AB,BC,AC – стороны треугольника |
| P – полупериметр $$ P = {AB + BC + AC \over 2} $$ | |
| R - радиус вписанной окружности |
Радиус вписанной окружности в равносторонний треугольник
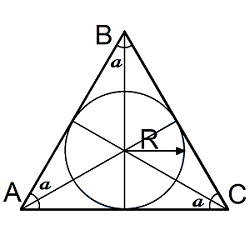
| Где: | AB,BC,AC – равные стороны треугольника |
| R - радиус вписанной окружности |
Радиус вписанной окружности равнобедренного треугольник

| Где: | AB,BC – равные стороны треугольника |
| AC – основание треугольника | |
| R - радиус вписанной окружности | |
| h – высота треугольника | |
| α – угол при основании треугольника |
Радиус вписанной окружности в прямоугольном треугольнике
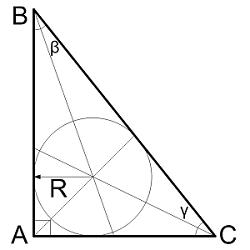
| Где: | AB,AC – катеты треугольника |
| BC – гипотенуза треугольника | |
| R - радиус вписанной окружности |
Длина окружности, L
$$ L = 2 * \pi * R $$Площадь окружности, S
$$ S = \pi * R^2 $$Углы треугольника
В произвольном треугольнике

- Если известны два угла,(∠ α, ∠ β) $$ ∠ γ = 180° - ∠ α - ∠ β $$
- Если известны три стороны $$ ∠ α = {AB^2 + AC^2 - BC^2 \over 2 * AB * AC} $$ $$ ∠ β = {AB^2 + BC^2 - AC^2 \over 2 * AB * BC} $$ $$ ∠ γ = {AC^2 + BC^2 - AB^2 \over 2 * AC * BC} $$
Углы в прямоугольном треугольнике